Notes from Mathilde Scholl 1904–1906
GA 91
9 November 1904, Berlin
Automated Translation
4. Sine, Cosine, Tangent, Cotangent
You can plot the angle Alpha a degree.
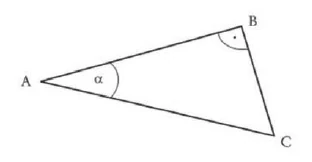
\(BC:AC\) – The ratio \(BC:AC\) is the ratio of the angle Alpha. The ratio is called the sin. (sine) of the angle. (\(AC:AB =\) cosine of Alpha)
\(BC:AC = \sin(\alpha)\)
\(AB:AC = \cos(\alpha)\)
\(BC:AB \tan(\alpha) = tg \alpha\)(\(BC:AB = \)tangent \(a\))
\(AB:BC \cot(\alpha)\) (\(AB:BC =\) cotangent \(a\))
You can determine a crooked line in a plane by calculating the distances between it and two straight lines. This method was first used in the last few centuries, by Cartesius. This method is called analytical geometry.
\(x^2 + y^2 = r^2 =\) the equation of the circle.
By determining the lawfulness of the distance on a particular system of intersecting lines, you get the circle.
(0\) is the center of the coordinate axis system. The ancients (Ptolemy) assumed the center of the earth, but Copernicus assumed the sun. He related everything to the Sun. However, he still took into account the fact that the Earth has its own motion in addition to its motion around the Sun, and that this motion is like the Earth's motion around the Sun. In schools, the third sentence of Copernicus is usually left out. In the Copernican system, the Earth actually moves in a helical path (Rod of Hermes).
Ptolemy's system was based on the astral plan. Copernicus's discovery meant that the relative motion of the planetary system was based on a different point of origin (the physical point of origin).
In Dante's Divine Comedy, everything is based on the astral plan; the Earth is the center.
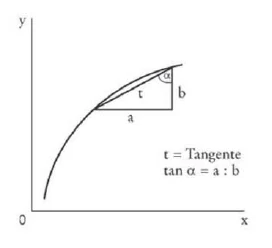
At the angle you can see the curvature of the line. The mathematician determines the angle according to the tangent. With each new distance, the tangent becomes different, larger or smaller.
tan a is absolutely variable with respect to the curve at very small distances. Then tan a is called a differential quotient. One goes from finite quantities to infinitely small quantities. Newton also called it flexion calculus (calculus of motion). Leibniz made the discovery at the same time. It was necessary to find the infinite on the physical plane itself.
\(\tan(\alpha) = \frac{x}{y}\) (if \(a\) and \(b\) are variable)

Two lines going to infinity, between them an infinitely large area.
Fl. \((ab) = \infty\) (infinitely large)
Fl. \((ac)= \infty =2 \infty\)
(Dividing one infinity by the other gives \(2\))
\(\frac{\infty}{\infty} = 2\)
An infinite straight line is a circle. However, this is not possible in three-dimensional space because it would take an infinite amount of time. If it is not a three-dimensional but a two-dimensional space, then it is different. Then time itself is the fourth dimension. Then not only movement in that direction takes place, but also another change. Suppose you move in one direction (a ball that gets bigger and bigger). Then, when the ball has reached a certain size, it will be possible for the ball to diverge on the other side. But then there must have been forces holding it together. In the astral space, the effect as a fourth dimension is added.
4. Sinus, Cosinus, Tangens, Kotangens
Es lassen sich im Winkel Alpha a Grade auftragen.

\(BC:AC\) — Durch das Verhältnis \(BC:AC\) ist das Verhältnis des Winkels Alpha bezeichnet. Das Verhältnis wird der sin. (Sinus) des Winkels genannt. (\(AC:AB =\) Cosinus zu Alpha)
\(BC:AC = \sin(\alpha)\)
\(AB:AC = \cos(\alpha)\)
\(BC:AB \tan(\alpha) = tg \alpha\)(\(BC:AB = \)Tangens \(a\))
\(AB:BC \cot(\alpha)\) (\(AB:BC =\) Kotangens \(a\))

Man kann eine krumme Linie in der Ebene bestimmen, wenn man, sie auf zwei gerade Linien beziehend, die Abstände berechnet. Diese Methode ist zuerst in den letzten Jahrhunderten angewendet worden, von Cartesius an. Diese Methode nennt man analytische Geometrie.
\(x^2 + y^2 = r^2 =\) die Gleichung des Kreises.
Indem man auf ein bestimmtes System von schneidenden Graden die Gesetzmäßigkeit der Entfernung bestimmt, bekommt man den Kreis.
\(0\) ist der Mittelpunkt des Koordinaten-Achsensystems. Die Alten (Ptolemäus) haben den Mittelpunkt der Erde angenommen, Kopernikus aber die Sonne. Er hat alles auf die Sonne bezogen. Er hat aber noch berücksichtigt, dass die Erde eine Eigenbewegung hat zu einer Bewegung um die Sonne und eine wie die Bewegung der Erde um die Sonne. In der Schule wird der dritte Satz des Kopernikus gewöhnlich ausgelassen. Im Sinne des Kopernikus bewegt sich die Erde in Wirklichkeit in einer Schraubenlinie (Stab des Hermes).
Das System des Ptolemäus bezog sich auf den Astralplan. Die Tat des Kopernikus bedeutet ein Beziehen der relativen Bewegung des Planetensystems auf einen anderen Ausgangspunkt (den physischen Ausgangspunkt).
In Dantes Göttlicher Komödie ist alles auf den Astralplan bezogen; da ist die Erde der Mittelpunkt.

An dem Winkel kann man erkennen die Krümmung der Linie. Der Mathematiker bestimmt den Winkel nach der Tangente. Mit jedem neuen Abstand wird die Tangente anders, größer oder kleiner.
tan a ist bei sehr kleinen Abständen absolut variabel in Bezug auf die Kurve. Dann heißt tan a ein Differentialquotient. Man geht über von endlichen Größen zu unendlich kleinen Größen. Newton nannte es auch Flexionsrechnung (Bewegungsrechnung). Leibniz machte die Entdeckung zu gleicher Zeit. Es war notwendig, auf dem physischen Plan selbst das Unendliche zu finden.
\(\tan(\alpha) = \frac{x}{y}\) (wenn \(a\) und \(b\) veränderlich sind)

Zwei ins Unendliche gehende Linien, dazwischen eine unendlich große Fläche.
Fl. \((ab) = \infty\) (unendlich groß)
Fl. \((ac)= \infty =2 \infty\)
(Die eine Unendlichkeit durch die andere dividiert gibt \(2\))
\(\frac{\infty}{\infty} = 2\)
Eine unendliche gerade Linie ist ein Kreis. Dies ist aber im dreidimensionalen Raum nicht möglich, weil dazu eine unendliche Zeit gehörte. Wenn es sich nicht um einen dreidimensionalen, sondern um einen zweidimensionalen Raum handelt, dann ist die Sache anders. Dann ist die Zeit selbst die vierte Dimension. Dann findet nicht nur ein Bewegen nach dieser Richtung statt, sondern auch eine andere Veränderung. Man nehme an, man bewege sich in einer Richtung (eine Kugel, die immer größer und größer wird). Dann wird, wenn die Kugel eine bestimmte Größe erreicht hat, es möglich sein, dass die Kugel auf der anderen Seite auseinanderläuft. Dann müssen aber Kräfte dagewesen sein, die sie zusammengehalten haben. Im Astralraum kommt die Wirkung als vierte Dimension hinzu.

