The Light Course
GA 320
Lecture I
23 December 1919, Stuttgart
My dear Friends,
After the words which have just been read out, some of which were written over 30 years ago, I would like to say that in the short time at our disposal I shall at most be able to contribute a few side-lights which may help you in forming your outlook upon Nature. I hope that in no very distant future we shall be able to continue. On this occasion, as you must also realize, I was only told that this lecture-course was hoped-for after my arrival here. What I can therefore give during these days will be no more than an episode.
What I am hoping to contribute may well be of use to those of you who are teachers and educators—not to apply directly in your lessons, but as a fundamental trend and tendency in Science, which should permeate your teaching. In view of all the aberrations to which the Science of Nature in our time has been subject, for the teacher and educator it is of great importance to have the right direction of ideas, at any rate in the background.
To the words which our friend Dr. Stein has kindly been recalling, I may add one more. It was in the early nineties. The Frankfurter Freier Hochstift had invited me to speak on Goethe's work in Science. I then said in introduction that I should mainly confine myself to his work in the organic Sciences. For to carry Goethe's world-conception into our physical and chemical ideas, was as yet quite impossible. Through all that lives and works in the Physics and Chemistry of today, our scientists are fated in regard, whatever takes its start from Goethe in this realm, as being almost unintelligible from their point of view. Thus, I opined, we shall have to wait till physicists and chemists will have witnessed—by their own researches—a kind of “reductio ad absurdum” of the existing theoretic structure of their Science. Then and then only will Goethe's outlook come into its own, also in this domain.
I shall attempt in these lectures to establish a certain harmony between what we may call the experimental side of Science and what concerns the outlook, the idea, the fundamental views which we can gain on the results of experiment. Today, by way of introduction,—and, as the saying goes, “theoretically”—I will put forward certain aspects that shall help our understanding. In today's lecture it will be my specific aim to help you understand that contrast between the current, customary science and the kind of scientific outlook which can be derived from Goethe's general world-outlook. We must begin by reflecting, perhaps a little theoretically, upon the premisses of present-day scientific thinking altogether. The scientists who think of Nature in the customary manner of our time, generally have no very clear idea of what constitutes the field of their researches. “Nature” has grown to be a rather vague and undefined conception. Therefore we will not take our start from the prevailing idea of what Nature is, but from the way in which the scientist of modern time will generally work. Admittedly, this way of working is already undergoing transformation, and there are signs which we may read as the first dawning of a new world-outlook. Yet on the whole, what I shall characterize (though in a very brief introductory outline) may still be said to be prevailing.
The scientist today seeks to approach Nature from three vantage-points. In the first place he is at pains to observe Nature in such a way that from her several creatures and phenomena he may form concepts of species, kind and genus. He sub-divides and classifies the beings and phenomena of Nature. You need only recall how in external, sensory experience so many single wolves, single hyenas, single phenomena of warmth, single phenomena of electricity are given to the human being, who thereupon attempts to gather up the single phenomena into kinds and species. So then he speaks of the species “wolf” or “hyena”, likewise he classifies the phenomena into species, thus grouping and comprising what is given, to begin with, in many single experiences. Now we may say, this first important activity is already taken more or less unconsciously for granted. Scientists in our time do not reflect that they should really examine how these “universals”, these general ideas, are related to the single data.
The second thing, done by the man of today in scientific research, is that he tries by experiment, or by conceptual elaboration of the results of experiment, to arrive at what he calls the “causes” of phenomena. Speaking of causes, our scientists will have in mind forces or substances or even more universal entities. They speak for instance of the force of electricity, the force of magnetism, the force of heat or warmth, and so on. They speak of an unknown “ether” or the like, as underlying the phenomena of light and electricity. From the results of experiment they try to arrive at the properties of this ether. Now you are well aware how very controversial is all that can be said about the “ether” of Physics. There is one thing however to which we may draw attention even at this stage. In trying, as they put it, to go back to the causes of phenomena, the scientists are always wanting to find their way from what is known into some unknown realm. They scarcely ever ask if it is really justified thus to proceed from the known to the unknown. They scarcely trouble, for example, to consider if it is justified to say that when we perceive a phenomenon of light or colour, what we subjectively describe as the quality of colour is the effect on us, upon our soul, our nervous apparatus, of an objective process that is taking place in the universal ether—say a wave-movement in the ether. They do not pause to think, whether it is justified thus to distinguish (what is what they really do) between the “subjective” event and the “objective”, the latter being the supposed wave-movement in the ether, or else the interaction thereof with processes in ponderable matter.
Shaken though it now is to some extent, this kind of scientific outlook was predominant in the 19th century, and we still find it on all hands in the whole way the phenomena are spoken of; it still undoubtedly prevails in scientific literature to this day.
Now there is also a third way in which the scientist tries to get at the configuration of Nature. He takes the phenomena to begin with—say, such a simple phenomenon as that a stone, let go, will fall to earth, or if suspended by a string, will pull vertically down towards the earth. Phenomena like this the scientist sums up and so arrives at what he calls a “Law of Nature”. This statement for example would be regarded as a simple “Law of Nature”: “Every celestial body attracts to itself the bodies that are upon it”. We call the force of attraction Gravity or Gravitation and then express how it works in certain “Laws”. Another classical example are the three statements known as “Kepler's Laws”.
It is in these three ways that “scientific research” tries to get near to Nature. Now I will emphasize at the very outset that the Goethean outlook upon Nature strives for the very opposite in all three respects. In the first place, when he began to study natural phenomena, the classification into species and genera, whether of the creatures or of the facts and events of Nature, at once became problematical for Goethe. He did not like to see the many concrete entities and facts of Nature reduced to all these rigid concepts of species, family and genus; what he desired was to observe the gradual transition of one phenomenon into another, or of one form of manifestation of an entity into another. He felt concerned, not with the subdivision and classification into genera, but with the metamorphosis both of phenomena and of the several creatures. Also the quest of so-called “causes” in Nature, which Science has gone on pursuing ever since his time, was not according to Goethe's way of thinking. In this respect it is especially important for us to realize the fundamental difference between natural science and research as pursued today and on the other hand the Goethean approach to Nature.
The Science of our time makes experiments; having thus studied the phenomena, it then tries to form ideas about the so-called causes that are supposed to be there behind them;—behind the subjective phenomenon of light or colour for example, the objective wave-movement in the ether. Not in this style did Goethe apply scientific thinking. In his researches into Nature he does not try to proceed from the so-called “known” to the so-called “unknown”. He always wants to stay within the sphere of what is known, nor in the first place is he concerned to enquire whether the latter is merely subjective, or objective. Goethe does not entertain such concepts as of the “subjective” phenomena of colour and the “objective” wave-movements in outer space. What he beholds spread out in space and going on in time is for him one, a single undivided whole. He does not face it with the question, subjective or objective? His use of scientific thinking and scientific method is not to draw conclusions from the known to the unknown; he will apply all thinking and all available methods to put the phenomena themselves together till in the last resort he gets the kind of phenomena which he calls archetypal,—the Ur-phenomena. These archetypal phenomena—once more, regardless of “subjective or objective”—bring to expression what Goethe feels is fundamental to a true outlook upon Nature and the World. Goethe therefore remains amid the sequence of actual phenomena; he only sifts and simplifies them and then calls “Ur-phenomenon” the simplified and clarified phenomenon, ideally transparent and comprehensive.
Thus Goethe looks upon the whole of scientific method—so to call it—purely and simply as a means of grouping the phenomena. Staying amid the actual phenomena, he wants to group them in such a way that they themselves express their secrets. He nowhere seeks to recur from the so-called “known” to an “unknown” of any kind. Hence too for Goethe in the last resort there are not what may properly be called “Laws of Nature”. He is not looking for such Laws. What he puts down as the quintessence of his researches are simple facts—the fact, for instance, of how light will interact with matter that is in its path. Goethe puts into words how light and matter interact. That is no “law”; it is a pure and simple fact. And upon facts like this he seeks to base his contemplation, his whole outlook upon Nature. What he desires, fundamentally, is a rational description of Nature. Only for him there is a difference between the mere crude description of a phenomenon as it may first present itself, where it is complicated still and untransparent, and the description which emerges when one has sifted it, so that the simple essentials and they alone stand out. This then—the Urphenomenon—is what Goethe takes to be fundamental, in place of the unknown entities or the conceptually defined “Laws” of customary Science.
One fact may throw considerable light on what is seeking to come into our Science by way of Goetheanism, and on what now obtains in Science. It is remarkable: few men have ever had so clear an understanding of the relation of the phenomena of Nature to mathematical thinking as Goethe had. Goethe himself not having been much of a mathematician, this is disputed no doubt. Some people think he had no clear idea of the relation of natural phenomena to those mathematical formulations which have grown ever more beloved in Science, so much so that in our time they are felt to be the one and only firm foundation. Increasingly in modern time, the mathematical way of studying the phenomena of Nature—I do not say directly, the mathematical study of Nature; it would not be right to put it in these words, but the study of natural phenomena in terms of mathematical formulae—has grown to be the determining factor in the way we think even of Nature herself.
Concerning these things we really must reach clarity. You see, dear Friends, along the accustomed way of approach to Nature we have three things to begin with—things that are really exercised by man before he actually reaches Nature. The first is common or garden Arithmetic. In studying Nature nowadays we do a lot of arithmetic—counting and calculating. Arithmetic—we must be clear on this—is something man understands on its own ground, in and by itself. When we are counting it makes no difference what we count. Learning arithmetic, we receive something which, to begin with, has no reference to the outer world. We may count peas as well as electrons. The way we recognize that our methods of counting and calculating are correct is altogether different from the way we contemplate and form conclusions about the outer processes to which our arithmetic is then applied.
The second of the three to which I have referred is again a thing we do before we come to outer Nature. I mean Geometry,—all that is known by means of pure Geometry. What a cube or an octahedron is, and the relations of their angles,—all these are things which we determine without looking into outer Nature. We spin and weave them out of ourselves. We may make outer drawings on them, but this is only to serve mental convenience, not to say inertia. Whatever we may illustrate by outer drawings, we might equally well imagine purely in the mind. Indeed it is very good for us to imagine more of these things purely in the mind, using the crutches of outer illustration rather less. Thus, what we have to say concerning geometrical form is derived from a realm which, to begin with, is quite away from outer Nature. We know what we have to say about a cube without first having had to read it in a cube of rock-salt. Yet in the latter we must find it. So we ourselves do something quite apart from Nature and then apply it to the latter.
And then there is the third thing which we do, still before reaching outer Nature. I am referring to what we do in “Phoronomy” so-called, or Kinematics, i.e. the science of Movement. Now it is very important for you to be clear on this point,—to realize that Kinematics too is, fundamentally speaking, still remote from what we call the “real” phenomena of Nature. Say I imagine an object to be moving from the point \(a\) to the point \(b\) (Figure 1a). I am not looking at any moving object; I just imagine it. Then I can always imagine this movement from \(a\) to \(b\), indicated by an arrow in the figure, to be compounded of two distinct movements. Think of it thus: the point \(a\) is ultimately to get to \(b\), but we suppose it does not go there at once. It sets out in this other direction and reaches \(c\). If it then subsequently moves from \(c\) to \(b\), it does eventually get to \(b\). Thus I can also imagine the movement from \(a\) to \(b\) so that it does not go along the line \(ab\) but along the line, or the two lines, \(ac\) and \(cb\). The movement \(ab\) is then compounded of the movements \(ac\) and \(cb\), i.e. of two distinct movements. You need not observe any process in outer Nature; you can simply think it—picture it to yourself in thought—how that the movement from \(a\) to \(b\) is composed of the two other movements. That is to say, in place of the one movement the two other movements might be carried out with the same ultimate effect. And when in thinking I picture this. The thought—the mental picture—is spun out of myself. I need have made no outer drawing; I could simply have instructed you in thought to form the mental picture; you could not but have found it valid. Yet if in outer Nature there is really something like the point \(a\)—perhaps a little ball, a grain of shot—which in one instance moves from \(a\) to \(b\) and in another from \(a\) to \(c\) and then from \(c\) to \(b\), what I have pictured to myself in thought will really happen. So then it is in kinematics, in the science of movement also; I think the movements to myself, yet what I think proves applicable to the phenomena of Nature and must indeed hold good among them.
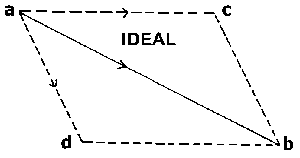
Thus we may truly say: In Arithmetic, in Geometry and in Phoronomy or Kinematics we have the three preliminary steps that go before the actual study of Nature. Spun as they are purely out of ourselves, the concepts which we gain in all these three are none the less valid for what takes place in real Nature.
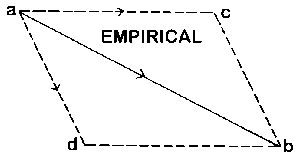
And now I beg you to remember the so-called Parallelogram of forces, (Figure 1b). This time, the point a will signify a material thing—some little grain of material substance. I exert a force to draw it on from \(a\) to \(b\). Mark the difference between the way I am now speaking and the way I spoke before. Before, I spoke of movement as such; now I am saying that a force draws the little ball from \(a\) to \(b\). Suppose the measure of this force, pulling from \(a\) to \(b\), to be five grammes; you can denote it by a corresponding length in this direction. With a force of five grammes I am pulling the little ball from \(a\) to \(b\). Now I might also do it differently. Namely I might first pull with a certain force from \(a\) to \(c\). Pulling from \(a\) to \(c\) (with a force denoted by this length) I need a different force than when I pulled direct from \(a\) to \(b\). Then I might add a second pull, in the direction of the line from \(c\) to \(b\), and with a force denoted by the length of this line. Having pulled in the first instance from a towards \(b\) with a force of five grammes, I should have to calculate from this figure, how big the pull \(ac\) and also how big the pull \(cd\) would have to be. Then if I pulled simultaneously with forces represented by the lines \(ac\) and \(ad\) of the parallelogram, I should be pulling the object along in such a way that it eventually got to \(b\); thus I can calculate how strongly I must pull towards \(c\) and \(d\) respectively. Yet I cannot calculate this in the same way as I did the displacements in our previous example. What I found previously (as to the movement pure and simple), that I could calculate, purely in thought. Not so when a real pull, a real force is exercised. Here I must somehow measure the force; I must approach Nature herself; I must go on from thought to the world of facts. If once you realize this difference between the Parallelogram of Movements and that of Forces, you have a clear and sharp formulation of the essential difference between all those things that can be determined within the realm of thought, and those that lie beyond the range of thoughts and mental pictures. You can reach movements but not forces with your mental activity. Forces you have to measure in the outer world. The fact that when two pulls come into play—the one from \(a\) to \(c\), the other from \(a\) to \(d\),—the thing is actually pulled from \(a\) to \(b\) according to the Parallelogram of Forces, this you cannot make sure of in any other way than by an outer experiment. There is no proof by dint of thought, as for the Parallelogram of Movements. It must be measured and ascertained externally. Thus in conclusion we may say: while we derive the parallelogram of movements by pure reasoning, the parallelogram of forces must be derived empirically, by dint of outer experience. Distinguishing the parallelogram of movements and that of forces, you have the difference—clear and keen—between Phoronomy and Mechanics, or Kinematics and Mechanics. Mechanics has to do with forces, no mere movements; it is already a Natural Science. Mechanics is concerned with the way forces work in space and time. Arithmetic, Geometry and Kinematics are not yet Natural Sciences in the proper sense. To reach the first of the Natural Sciences, which is Mechanics, we have to go beyond the life of ideas and mental pictures.
Even at this stage our contemporaries fail to think clearly enough. I will explain by an example, how great is the leap from kinematics into mechanics. The kinematical phenomena can still take place entirely within a space of our own thinking; mechanical phenomena on the other hand must first be tried and tested by us in the outer world. Our scientists however do not envisage the distinction clearly. They always tend rather to confuse what can still be seen in purely mathematical ways, and what involves realities of the outer world. What, in effect, must be there, before we can speak of a parallelogram of forces? So long as we are only speaking of the parallelogram of movements, no actual body need be there; we need only have one in our thought. For the parallelogram of forces on the other hand there must be a mass—a mass, that possesses weight among other things. This you must not forget. There must be a mass at the point a, to begin with. Now we may well feel driven to enquire: What then is a mass? What is it really? And we shall have to admit: Here we already get stuck! The moment we take leave of things which we can settle purely in the world of thought so that they then hold good in outer Nature, we get into difficult and uncertain regions. You are of course aware how scientists proceed. Equipped with arithmetic, geometry and kinematics, to which they also add a little dose of mechanics, they try to work out a mechanics of molecules and atoms; for they imagine what is called matter to be thus sub-divided, In terms of this molecular mechanics they then try to conceive the phenomena of Nature, which, in the form in which they first present themselves, they regard as our own subjective experience.
We take hold of a warm object, for example. The scientist will tell us: What you are calling the heat or warmth is the effect on your own nerves. Objectively, there is the movement of molecules and atoms. These you can study, after the laws of mechanics. So then they study the laws of mechanics, of atoms and molecules; indeed, for a long time they imagined that by so doing they would at last contrive to explain all the phenomena of Nature. Today, of course, this hope is rather shaken. But even if we do press forward to the atom with our thinking, even then we shall have to ask—and seek the answer by experiment—How are the forces in the atom? How does the mass reveal itself in its effects,—how does it work? And if you put this question, you must ask again: How will you recognize it? You can only recognize the mass by its effects.
The customary way is to recognize the smallest unit bearer of mechanical force by its effect, in answering this question: If such a particle brings another minute particle—say, a minute particle of matter weighing one gramme—into movement, there must be some force proceeding from the matter in the one, which brings the other into movement. If then the given mass brings the other mass, weighing one gramme, into movement in such a way that the latter goes a centimetre a second faster in each successive second, the former mass will have exerted a certain force. This force we are accustomed to regard as a kind of universal unit. If we are then able to say of some force that it is so many times greater than the force needed to make a gramme go a centimetre a second quicker every second, we know the ratio between the force in question and the chosen universal unit. If we express it as a weight, it is 0.001019 grammes' weight. Indeed, to express what this kind of force involves, we must have recourse to the balance—the weighing-machine. The unit force is equivalent to the downward thrust that comes into play when 0.001019 grammes are being weighed. So then I have to express myself in terms of something very outwardly real if I want to approach what is called “mass” in this Universe. Howsoever I may think it out, I can only express the concept “mass” by introducing what I get to know in quite external ways, namely a weight. In the last resort, it is by a weight that I express the mass, and even if I then go on to atomize it, I still express it by a weight.
I have reminded you of all this, in order clearly to describe the point at which we pass, from what can still be determined “a priori”, into the realm of real Nature. We need to be very clear on this point. The truths of arithmetic, geometry and kinematics,—these we undoubtedly determine apart from external Nature. But we must also be clear, to what extent these truths are applicable to that which meets us, in effect, from quite another side—and, to begin with, in mechanics. Not till we get to mechanics, have we the content of what we call “phenomenon of Nature”.
All this was clear to Goethe. Only where we pass on from kinematics to mechanics can we begin to speak at all of natural phenomena. Aware as he was of this, he knew what is the only possible relation of Mathematics to Natural Science, though Mathematics be ever so idolized even for this domain of knowledge.
To bring this home, I will adduce one more example. Even as we may think of the unit element, for the effects of Force in Nature, as a minute atom-like body which would be able to impart an acceleration of a centimetre per second per second to a gramme-weight, so too with every manifestation of Force, we shall be able to say that the force proceeds from one direction and works towards another. Thus we may well grow accustomed—for all the workings of Nature—always to look for the points from which the forces proceed. Precisely this has grown habitual, nay dominant, in Science. Indeed in many instances we really find it so. There are whole fields of phenomena which we can thus refer to the points from which the forces, dominating the phenomena, proceed. We therefore call such forces “centric forces”, inasmuch as they always issue from point-centres. It is indeed right to think of centric forces wherever we can find so many single points from which quite definite forces, dominating a given field of phenomena, proceed. Nor need the forces always come into play. It may well be that the point-centre in question only bears in it the possibility, the potentiality as it were, for such a play of forces to arise, whereas the forces do not actually come into play until the requisite conditions are fulfilled in the surrounding sphere. We shall have instances of this during the next few days. It is as though forces were concentrated at the points in question,—forces however that are not yet in action. Only when we bring about the necessary conditions, will they call forth actual phenomena in their surroundings. Yet we must recognize that in such point or space forces are concentrated, able potentially to work on their environment.
This in effect is what we always look for, when speaking of the World in terms of Physics. All physical research amounts to this: we follow up the centric forces to their centres; we try to find the points from which effects can issue, For this kind of effect in Nature, we are obliged to assume that there are centres, charged as it were with possibilities of action in certain directions. And we have sundry means of measuring these possibilities of action; we can express in stated measures, how strongly such a point or centre has the potentiality of working. Speaking in general terms, we call the measure of a force thus centred and concentrated a “potential” or “potential force”. In studying these effects of Nature we then have to trace the potentials of the centric forces,—so we may formulate it. We look for centres which we then investigate as sources of potential forces.
Such, in effect, is the line taken by that school of Science which is at pains to express everything in mechanical terms. It looks for centric forces and their potentials. In this respect our need will be to take one essential step—out into actual Nature—whereby we shall grow fully conscious of the fact: You cannot possibly understand any phenomenon in which Life plays a part if you restrict yourself to this method, looking only for the potentials of centric forces. Say you were studying the play of forces in an animal or vegetable embryo or germ-cell; with this method you would never find your way. No doubt it seems an ultimate ideal to the Science of today, to understand even organic phenomena in terms of potentials, of centric forces of some kind. It will be the dawn of a new world-conception in this realm when it is recognized that the thing cannot be done in this way, Phenomena in which Life is working can never be understood in terms of centric forces. Why, in effect,—why not? Diagrammatically, let us here imagine that we are setting out to study transient, living phenomena of Nature in terms of Physics. We look for centres,—to study the potential effects that may go out from such centres. Suppose we find the effect. If I now calculate the potentials, say for the three points \(a\), \(b\) and \(c\), I find that \(a\) will work thus and thus on \(A\), \(B\) and \(C\), or \(c\) on \(A'\), \(B'\) and \(C'\); and so on. I should thus get a notion of how the integral effects will be, in a certain sphere, subject to the potentials of such and such centric forces. Yet in this way I could never explain any process involving Life. In effect, the forces that are essential to a living thing have no potential; they are not centric forces. If at a given point \(d\) you tried to trace the physical effects due to the influences of \(a\), \(b\) and \(c\), you would indeed be referring to the effects to centric forces, and you could do so. But if you want to study the effects of Life you can never do this. For these effects, there are no centres such as \(a\) or \(b\) or \(c\). Here you will only take the right direction with your thinking when you speak thus: Say that at \(d\) there is something alive. I look for the forces to which the life is subject. I shall not find them in \(a\), nor in \(b\), nor in \(c\), nor when I go still farther out. I only find them when as it were I go to the very ends of the world—and, what is more, to the entire circumference at once. Taking my start from \(d\), I should have to go to the outermost ends of the Universe and imagine forces to the working inward from the spherical circumference from all sides, forces which in their interplay unite in \(d\). It is the very opposite of the centric forces with their potentials. How to calculate a potential for what works inward from all sides, from the infinitudes of space? In the attempt, I should have to dismember the forces; one total force would have to be divided into ever smaller portions. Then I should get nearer and nearer the edge of the World:—the force would be completely sundered, and so would all my calculation. Here in effect it is not centric forces; it is cosmic, universal forces that are at work. Here, calculation ceases.
Once more, you have the leap—the leap, this time, from that in Nature which is not alive to that which is. In the investigation of Nature we shall only find our way aright if we know what the leap is from Kinematics to Mechanics, and again what the leap is from external, inorganic Nature into those realms that are no longer accessible to calculation,—where every attempted calculation breaks asunder and every potential is dissolved away. This second leap will take us from external inorganic Nature into living Nature, and we must realize that calculation ceases where we want to understand what is alive.
Now in this explanation I have been neatly dividing all that refers to potentials and centric forces and on the other hand all that leads out into the cosmic forces. Yet in the Nature that surrounds us they are not thus apart. You may put the question: Where can I find an object where only centric forces work with their potentials, and on the other hand where is the realm where cosmic forces work, which do not let you calculate potentials? An answer can indeed be given, and it is such as to reveal the very great importance of what is here involved. For we may truly say: All that Man makes by way of machines—all that is pieced together by Man from elements supplied by Nature—herein we find the purely centric forces working, working according to their potentials. What is existing in Nature outside us on the other hand—even in inorganic Nature—can never be referred exclusively to centric forces. In Nature there is no such thing; it never works completely in that way: Save in the things made artificially by Man, the workings of centric forces and cosmic are always flowing together in their effects. In the whole realm of so-called Nature there is nothing in the proper sense un-living. The one exception is what Man makes artificially; man-made machines and mechanical devices.
The truth of this was profoundly clear to Goethe. In him, it was a Nature-given instinct, and his whole outlook upon Nature was built upon this basis. Herein we have the quintessence of the contrast between Goethe and the modern Scientist as represented by Newton. The scientists of modern time have only looked in one direction, always observing external Nature in such a way as to refer all things to centric forces,—as it were to expunge all that in Nature which cannot be defined in terms of centric forces and their potentials. Goethe could not make do with such an outlook. What was called “Nature” under this influence seemed to him a void abstraction. There is reality for him only where centric forces and peripheric or cosmic forces are alike concerned,—where there is interplay between the two. On this polarity, in the last resort, his Theory of Colour is also founded, of which we shall be speaking in more detail in the next few days.
All this, dear Friends, I have been saying to the end that we may understand how the relation is even of Man himself to all his study and contemplation of Nature.—We must be willing to bethink ourselves in this way, the more so as the time has come at last when the impossibility of the existing view of Nature is beginning to be felt—subconsciously, at least. In some respects there is at least a dawning insight that these things must change. People begin to see that the old view will serve no longer. No doubt they are still laughed at when they say so, but the time is not so distant when this derision too will cease. The time is not so very distant when even Physics will be such as to enable one to speak in Goethe's sense. Men will perhaps begin to speak of Colour, for example, more in Goethe's spirit when another rampart has been shaken, which, though reputed impregnable, is none the less beginning to be undermined. I mean the theory of Gravitation. Ideas are now emerging almost every year, shaking the old Newtonian conceptions about Gravitation, and bearing witness how impossible it is to make do with these old conceptions, built as they are on the exclusive mechanism of centric forces.
Today, I think, both teachers who instruct the young, and altogether those who want to play an active, helpful part in the development of culture, must seek a clearer picture of Man's relation to Nature and how it needs to be.

